图像变换

基本的图像变换有刚性变换(等距变换、欧式变换)、相似变换、仿射变换、射影变换(透视变换、投影变换)

刚性变化：只对图像进行平移与旋转，形状保持不变

欧式变换（等距变换）保持了向量的长度和夹角，相当于我们把一个刚体原封不动地进行移动或旋转，不改变它自身的样子

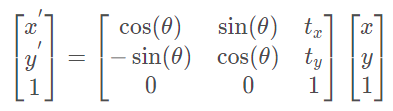
刚体变换矩阵

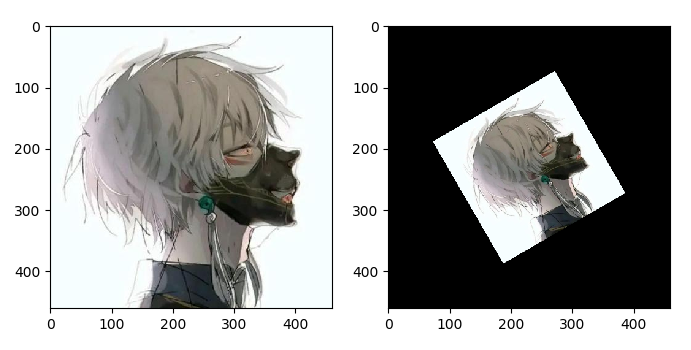
相似变换：等距变换与一个均匀缩放的复合；等距变换+ 均匀缩放，类似相似三角形，比例不变

相似变换比欧氏变换多了一个自由度，它允许物体进行均匀的放缩，其矩阵表示形式为：

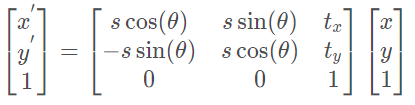
相似变换矩阵

import cv2
import matplotlib.pyplot as plt
import numpy as np

img = cv2.imread('/hone/chy/pic/git.png', 1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# print(img.shape)

# 得到相似变换的矩阵  # center：旋转中心 angle：旋转角度   scale：缩放比例
M = cv2.getRotationMatrix2D(center = (img.shape[0]/2,img.shape[1]/2),
                              angle = 30,
                              scale = 0.5) 

# 原图像按照相似矩阵进行相似变换  三个参数：原图像，相似矩阵，画布面积
img_rotate = cv2.warpAffine(img, M, (img.shape[0], img.shape[1]))

plt.figure(figsize=(8,8))
plt.subplot(1,2,1)
plt.imshow(img)
plt.subplot(1,2,2)
plt.imshow(img_rotate)
plt.show()

相似变换结果

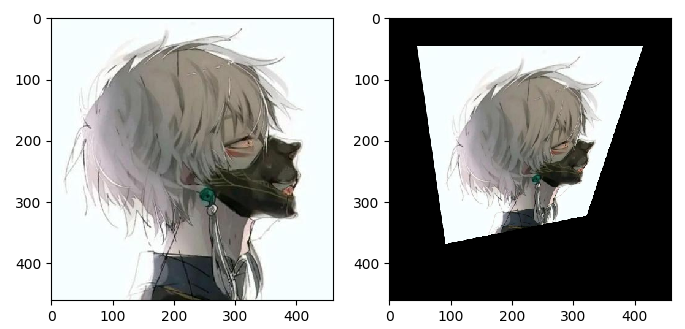
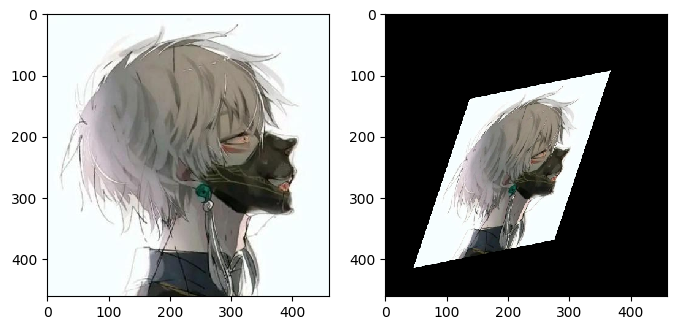
仿射变换：非齐次坐标下的一个非奇异线性变换与一个平移变换的复合，（即第三行是0,0,1）; 旋转+平移+缩放+切变，保持平行性

仿射变换只要求 A 是一个可逆矩阵，而不必是正交矩阵。仿射变换也叫正交投影。经过仿射变换之后，立方体就不再是方的了，但是各个面仍是平行四边形

性质：Parallel lines are still parallel lines（不再具有保角性，具有保平行性）
三个非共线的点对（6 parameters）确定一个仿射变换。

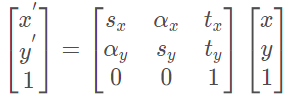
仿射变换矩阵

import cv2
import matplotlib.pyplot as plt
import numpy as np

# 3 Src(原始) Points + 3 Dst(目标) Points
# cols：列/长  rows：行/宽

img = cv2.imread('lenna.jpg', 1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# print(img.shape)

cols = img.shape[0]
rows = img.shape[1]

pt1 = np.float32([[0,0], [cols, 0], [0, rows]])
pt2 = np.float32([[cols*0.3, rows*0.3], [cols*0.8, rows*0.2], [cols*0.1, rows*0.9]])

# [[0,0], [cols, 0], [0, rows]] --> [[cols*0.3, rows*0.3], [cols*0.8, rows*0.2], [cols*0.1, rows*0.9]]
M = cv2.getAffineTransform(pt1, pt2)       # 仿射变换矩阵
dst = cv2.warpAffine(img, M, (cols, rows))

plt.figure(figsize=(8,8))
plt.subplot(1,2,1)
plt.imshow(img)
plt.subplot(1,2,2)
plt.imshow(dst)
plt.show()

仿射变换结果

射影变换:次坐标的一般非奇异线性变换。射影变换可以分解为相似变换，仿射变换，射影变换的复合，不保留平行性，保留重合关系、长度的交比

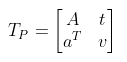
射影变换矩阵

它左上角为可逆矩阵 A，右上为平移 t，左下缩放 a^{T} 。由于采用齐坐标，当 v \neq 0 时吗我们可以对整个矩阵除于 v得到一个右下角为 1 的矩阵；否则，则得到右下角为 0 的矩阵。因此，2D 的射影变换一共有8个自由度，3D则共有15个自由度。

性质：Lines are still lines（不保角，不保平行，保直线性）
四个非共线的点对（8 parameters）确定一个透视变换

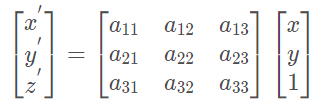
射影变换矩阵

import cv2
import matplotlib.pyplot as plt
import numpy as np

img = cv2.imread('lenna.jpg', 1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

width = img.shape[1]
height = img.shape[0]

pts1 = np.float32([[0,0], [width,0], [0,height], [width,height]])
pts2 = np.float32([[width*0.1,height*0.1], [width*0.9, width*0.1], [height*0.2,height*0.8], [width*0.7,height*0.7]])

M_warp = cv2.getPerspectiveTransform(pts1, pts2)     # 单应性矩阵
img_warp = cv2.warpPerspective(img, M_warp, (width, height))

plt.figure(figsize=(8,8))
plt.subplot(1,2,1)
plt.imshow(img)
plt.subplot(1,2,2)
plt.imshow(img_warp)
plt.show()