RANSAC算法简介
RANSAC是”RANdom SAmple Consensus”(随机采样一致)的缩写。它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数,它是一种不确定的算法—-它有一定的概率得出一个合理的结果;为了提高概率必须提高迭代次数。
RANSAC基本假设
- 数据由局内点组成, 例如,数据的分布可以用一些模型(比如直线方程)参数来解释;
- 局外点是不能适应该模型的参数;
- 除此之外的数据属于噪声;
局外点产生的原因有:噪声的极值;错误的测量方法;对数据的错误假设等;
RANSAC概述
RANSAC算法的输入时一组观测数据,一个可以解释或者适应于观测数据的参数化模型,一些可行的参数。
RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点,并用下述方法进行验证:
- 有一个模型适应于假定的局内点,即所有的未知参数都能从假设的局内点计算得出;
- 用1中得到的模型去测试所有的其它数据,如果某个点适用于估计的模型,认为他也是局内点;
- 如果有足够多的点呗归类为假设的局内点,那么估计的模型就足够合理;
- 然后,用所有假设的局内点去重新估计模型,因为它仅仅被初始的假设局内点估计过;
- 最后,通过估计局内点与模型的错误率来评估模型;
这个过程被重复执行固定的次数,每次产生的模型要么因为局内点太少而被抛弃,要么因为比现有的模型更好而被选用。
关于模型好坏算法实现上有两种方式:
- 规定一个点数,达到这个点数后,算这些点与模型间的误差,找误差最小的模型。 对应下面算法一
- 规定一个误差,找匹配模型并小于这个误差的所有点,匹配的点最多的模型,就是最好模型。 对应下面算法二
算法伪代码一:
输入:
data ---- 一组观测数据
model ---- 适应于数据的模型
n ---- 适用于模型的最少数据个数
k ---- 算法的迭代次数
t ---- 用于决定数据是否适应于模型的阈值
d ---- 判定模型是否适用于数据集的数据数目
输出:
best_model —— 跟数据最匹配的模型参数(如果没有找到,返回null)
best_consensus_set —— 估计出模型的数据点
best_error —— 跟数据相关的估计出的模型的错误
iterations = 0
best_model = null
best_consensus_set = null
best_error = 无穷大
while( iterations < k )
maybe_inliers = 从数据集中随机选择n个点
maybe_model = 适合于maybe_inliers的模型参数
consensus_set = maybe_inliers
for (每个数据集中不属于maybe_inliers的点)
if (如果点适合于maybe_model,并且错误小于t)
将该点添加到consensus_set
if (consensus_set中的点数大于d)
已经找到了好的模型, 现在测试该模型到底有多好
better_model = 适用于consensus_set中所有点的模型参数
this_error = better_model 究竟如何适合这些点的度量
if (this_error < best_error)
发现比以前好的模型,保存该模型直到更好的模型出现
best_model = better_model
best_consensus_set = consensus_set
best_error = this_error
iterations ++
函数返回best_model, best_consensus_set, best_error
RANSAC算法的可能变化包括以下几种:
- 如果发现一种足够好的模型(该模型有足够下的错误率), 则跳出主循环,这样节约不必要的计算;设置一个错误率的阈值,小于这个值就跳出循环;
- 可以直接从maybe_model计算this_error,而不从consensus_set重新估计模型,这样可能会节约时间,但是可能会对噪音敏感。
算法伪代码二:
输入:
data ---- 一组观测数据
numForEstimate ----- 初始模型需要的点数
delta ------ 判定点符合模型的误差
probability ----- 表示迭代过程中从数据集内随机选取出的点均为局内点的概率
输出:
best_model —— 跟数据最匹配的模型参数(如果没有找到,返回null)
best_consensus_set —— 估计出模型的数据点
k = 1000 //设置初始值
iterations = 0
best_model = null
best_consensus_set = null
while( iterations < k )
maybe_inliers = 从数据集中随机选择numForEstimate个点
maybe_model = 适合于maybe_inliers的模型参数,比如直线,取两个点,得直线方程
for (每个数据集中不属于maybe_inliers的点)
if (如果点适合于maybe_model,并且错误小于delta)
将该点添加到maybe_inliers
if(maybe_inliers的点数 > best_consensus_set 的点数) //找到更好的模型
best_model = maybe_model
best_consensus_set = maybe_inliers
根据公式k=log(1-p)/log(1-pow(w,n))重新计算k
iterations ++
函数返回best_model, best_consensus_set,
RANSAC参数
我们不得不根据特定的问题和数据集通过实验来确定参数t和d。然而参数k(迭代次数)可以从理论结果推断。当我们从估计模型参数时,用p表示一些迭代过程中从数据集内随机选取出的点均为局内点的概率;此时,结果模型很可能有用,因此p也表征了算法产生有用结果的概率。用w表示每次从数据集中选取一个局内点的概率,如下式所示: w = 局内点的数目 / 数据集的数目 通常情况下,我们事先并不知道w的值,但是可以给出一些鲁棒的值。假设估计模型需要选定n个点,wn是所有n个点均为局内点的概率;1 − wn是n个点中至少有一个点为局外点的概率,此时表明我们从数据集中估计出了一个不好的模型。 (1 − wn)k表示算法永远都不会选择到n个点均为局内点的概率,它和1-p相同。因此,
$$
1-p=\left(1-w^n\right)^k
$$
其中
p 表示置信度confidence
w 表示数据集中inlier占的比例
n 表示采样点数
k 表示需要迭代采样的最少次数
1 − wn 表示采样一次,n个点中至少有一个outlier的概率
(1 − wn)k 表示采样k次,n个点中至少有一个outlier的概率
因为p为采样k次,能有至少一次n个点都是inlier的概率
所以(1 − p)和(1 − wn)k相等时,k 为需要迭代采样的最少次数
下面是k的解析解:
$$
k=\frac{\log (1-p)}{\log \left(1-w^n\right)}
$$
值得注意的是,这个结果假设n个点都是独立选择的;也就是说,某个点被选定之后,它可能会被后续的迭代过程重复选定到。这种方法通常都不合理,由此推导出的k值被看作是选取不重复点的上限。例如,要从上图中的数据集寻找适合的直线,RANSAC算法通常在每次迭代时选取2个点,计算通过这两点的直线maybe_model,要求这两点必须唯一。
为了得到更可信的参数,标准偏差或它的乘积可以被加到k上。k的标准偏差定义为:
$$
S D(k)=\frac{\sqrt{1-w^n}}{w^n}
$$
RANSAC的函数接口 参照opencv来说主要需要3-4个参数(第四个不是必须的)
- 误差阈值ransacThreshold:区分inlier和outliner的依据
- 置信度confidence:设置之后代表RANSAC采样n次过程中会出现(至少一次)采样点数据集中的点都为内点的概率。这个值设置的太大,会增加采样次数。太小,会使结果不太理想。一般取0.95-0.99
- 最大采样迭代次数maxIters:为了防止一直在采样计算
- 最大精细迭代次数refineIters:在采样之后,选取最优解。可以增加精确优化,比如使用LM算法获得更优解。
以上4个参数,有三个是经验值。其中最大采样迭代次数maxIters是可以有数值解的。
RANSAC优点与缺点
RANSAC的优点是它能鲁棒的估计模型参数。例如,它能从包含大量局外点的数据集中估计出高精度的参数。
RANSAC的缺点是它计算参数的迭代次数没有上限;如果设置迭代次数的上限,得到的结果可能不是最优的结果,甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型,概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。
RANSAC只能从特定的数据集中估计出一个模型,如果存在两个(或多个)模型,RANSAC不能找到别的模型。如果有多个模型,可以先估算出一个,然后用剩余的数据重新运算,重复这个过程,直到没有模型。
参考文献
RANSAC应用
OpenCV中使用RANSAC算法实现多张图像拼接思路:
获取图像的特征点,将每张图片的特征点保存到一个vector中;
通过特征点匹配的方法,找到每张图片的共有特征点,并将其保存到一个vector中;
通过RANSAC算法求解出拼接的变换矩阵;
根据变换矩阵对每张图片进行仿射变换;
将拼接后的图片进行裁剪;
将裁剪后的图片拼接起来,最终得到拼接后的图片。
OpenCV中的solvePnPRansac函数和findHomography函数都具有RANSAC特性,该特性使算法对少量的错误数据鲁棒。
这两个函数利用RANSACPointSetRegistrator类实现RANSAC算法,但这个类并没有对外开放,因此只能通过阅读OpenCV源代码学习RANSAC算法的实现和使用。
类的实现在ptsetreg.cpp中,可通过调用precomp.hpp文件中的createRANSACPointSetRegistrator函数使用。此外,该文件还提供了createLMeDSPointSetRegistrator函数调用最小中值算法。
LMEDS算法概述(最小中值法:Least Median of Squares)
经典步骤
随机采样
计算模型参数
计算相对模型的点集偏差err,并求出偏差中值Med(err)
迭代2. 3.步直至获得符合阈值的最优解:Med(err)最小
精确优化模型参数(LM算法迭代优化)
LMedS的函数接口 参照opencv来说主要需要2-3个参数(第三个不是必须的)
置信度confidence:设置之后代表RANSAC采样n次过程中会出现(至少一次)采样点数据集中的点都为内点的概率,这个值设置的太大,会增加采样次数。太小,会使结果不太理想。一般取0.95-0.99
最大采样迭代次数maxIters:为了防止一直在采样计算
最大精细迭代次数refineIters:在采样之后,选取最优解。可以增加精确优化,比如使用LM算法获得更优解。
注意: 相对于RANSAC,LMedS有一个优点:不需要指定 - 误差阈值ransacThreshold:区分inlier和outliner的依据
RANSAC与LMEDS两者的区别
RANSAC的阈值在具有物理意义或者几何意义的时候比较容易确定,但是当阈值不具有这些特征的时候,就成了一个不太好调整的参数了。这时LMedS可以自适应迭代获得最优解。
此外,LMedS也能自适应获得inlier和outliner,公式如下:
$$
\hat{\sigma}=1.4826\left(1+\frac{5}{n-p}\right) \operatorname{med}_i \sqrt{r_i^2}
$$
其中
n 表示点集的个数
p 表示计算模型一次采样的点个数
ri2 表示误差
med(ri2 ) 表示误差中值
筛选条件为:
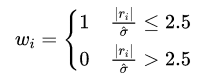
由于LMedS会需要对整个点集的err求中值,当点集很大的时候,求中值的过程会很消耗时间
霍夫变换(Hough)
霍夫变换是一种特征提取(feature extraction),被广泛应用在图像分析(image analysis)、计算机视觉(computer vision)以及数位影像处理(digital image processing)。霍夫变换是用来辨别找出物件中的特征,例如:线条。他的算法流程大致如下,给定一个物件、要辨别的形状的种类,算法会在参数空间(parameter space)中执行投票来决定物体的形状,而这是由累加空间(accumulator space)里的局部最大值(local maximum)来决定。
经典的霍夫变换是侦测图片中的直线,之后,霍夫变换不仅能识别直线,也能够识别任何形状,常见的有圆形、椭圆形。1981年,因为DanaH.Ballard的一篇期刊论文”Generalizing the Hough transform to detect arbitrary shapes”,让霍夫变换开始流行于计算机视觉界。



